HP 39g hp 39g+ (39g & 40g)_mastering the hp 39g+_English_E_F2224-90010.pdf - Page 89
that it rounds off to a smaller number than 1.03, which is
 |
View all HP 39g manuals
Add to My Manuals
Save this manual to your list of manuals |
Page 89 highlights
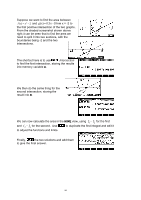
The problem lies in the fact that the slow convergence will mean that people will often try to graph this function for very large values of x. The first graph on the right shows the graph of this function for the domain of 0 to 100. The second graph shows how instability develops in the domain 0 to 1E11 (1×1011 ). This apparent instability is caused by the internal rounding of the calculator. It works to 16 bits accuracy, which means that it can store 12 significant digits (for reasons only of interest to programmers). This means that when you invert a really large number and add it to one, you lose a lot of accuracy. For example: if X = 2⋅85×1010 then 1/X is 2⋅5087719298×10-11. When you add 1 to this, the calculator is forced to discard all but the last decimal place. Thus 1 + 1/X = 1.00000000003 (rounded off from 1.00000000002508...) There are naturally a whole range of numbers which will all round off to the same value of 1.00000000003, so that (for that range of numbers) the expression (1+1/X)^X is equivalent mathematically (on the HP) to (1.00000000003)^X. This produces a short section of an exponential graph, which only looks linear because you don't see enough of it. Eventually the calculator reaches a value on the x axis which is large enough that it rounds off to a smaller number than 1.00000000003, which is 1.00000000002. This produces the sudden drop in the graph as the plot changes from a section of a 1.00000000003^X graph to a section of a 1.00000000002^X graph (which has a shallower gradient). This section is maintained until the next drop, and so on. Finally, at the value x = 2×1011 the inverted value is so small that 1+1/X becomes exactly 1 and the graph becomes horizontal. Of course this is completely the wrong value! Although this explanation may be beyond the level of many students it is quite important that they have some understanding of these ideas if they use the calculator to evaluate limits. The solution to all problems of this type is to simply be aware of their existence and to allow for them rather than simply accepting the results shown in the NUM view. 89