HP 40g hp 39g+ (39g & 40g)_mastering the hp 39g+_English_E_F2224-90010.pdf - Page 81

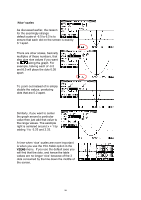
Integration: The algebraic indefinite integral Algebraic integration is also possible (for simple functions), in the following fashions: i. If done in the SYMB view of the Function aplet, then the integration must be done using the symbolic variable S1 (or S2, S3, S4 or S5). If done in this manner then the results are very good, except that there is no constant of integration 'c'. The screenshot right shows the results of defining F1( X ) = X 2 −1 and then ( ) F 2( X ) = ∫ 0, S1, X 2 −1, X , together with the results of the same thing after pressing the key (the result is placed in F3 only for convenience of viewing). All that is now necessary is to read '-S1+S1^3/3' as −x + x3 , or as it 3 should be read as x3 − x + c . 3 ii. If done in the HOME view, then S1 must again be used as the variable of integration. i.e. ∫ x2 −1 dx is entered as ∫ ( 1, S1, X2 - 1, X ). This is shown right, together with the results of highlighting the answer and pressing . The calculator assumes that X itself may be a function of some other variable and integrates accordingly as a 'partial integration' which, while mathematically correct, is not what most of us want. The way to simplify this answer to a better form is to highlight it, it, and press ENTER again, giving the result shown right. This is the result of the calculator performing the substitutions implied in the previous expression. 81