Sharp EL-733 EL-733A Operation Manual - Page 25
$571p5$5$64
 |
View all Sharp EL-733 manuals
Add to My Manuals
Save this manual to your list of manuals |
Page 25 highlights
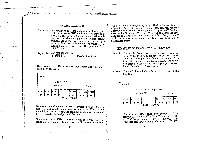
TVM Applications In working a TVM problem, you have to translate the financial language that you are used to dealing with to the simple language of the five TVM keys. When it comes to TVM problems, the calculator understands only the terms n, i, PV, FV, and PMT. All of the language that you may be used to working with (balloon payment, residual, points, coupon, the list goes on and on) has to be translated into these five terms. If you truly understand your particular financial language and if you know how to draw a cash-flow schedule based on that language, the translation is easy. Let's give it a try. A TYPICAL MORTGAGE (COMPUTING A PAYMENT) Example: As a realtor, you have a chance to sell a $1061000.00 house to a buyer that you have been showing houses to for the last couple of weeks. The buyer can come up with about $121000.00 as I a down payment, leaving about $94'000.00 to ; finance. The interest rate is hovering at around 10.5% APR. The term of a typical mortgage is 30 years. What will be the I payment on this loan? PV = 94'000.00 i=10.5+12 n=30x12 FV=0 I it 4'. v9 iv 354$5$571p5$5$64 PMT=? A couple questions may arise when you look at the above cash-flow schedule. First, how do you know that the period is monthly; where was that stated? And second, what is an APR, and how do you know that it needs to be divided by 12 in this case. THE 2nd PI KEY. MONTHLY PERIODS The answer to the first question is that the period should be stated in the description of the problem. However, usually if the period isn't explicitly stated in a description, you can assume it is monthly. In fact, the monthly period is so common that the second function 110 txl is provided above the (11 key on the EL-733A to speed up the conversion of years into months. Explanation: The cash-flow schedule of this problem is an easy one to draw. It is drawn here from the perspective of the borrower. To the borrower, the payment will be money going out each month which makes it a down-arrow (a negative value) on the cash-flow schedule. It is important, when drawing a cash-flow schedule, to pick one perspective, either that of the borrower or that of the lender, and to stick to that perspective throughout the problem. THE (-27r1fl KEY AND APR The answer to institutions (most the second question is that lending banks, the FHA, and finance companies) usually quote interest as a "nominal APR (Annual Percentage Rate)." They take the periodic rate that they use inpneeertidhoedtiosridcnoaalcgyuivelaeatnrio(aunnssuaAanlPldyRt1hw2e)iy.thmSmouuoltsniputhlayllyliytctobhmye ptfhioreusntndtuhimningbgiesyr otoouf